SF (HP-Prime)
Table of Contents

Description #
Calculates the Superformula for any angle Φ from Φ = 0 degree to Φ = 359 degrees.
\begin{equation} r(\phi) = \frac{1}{ \sqrt[n₁]{ \left| \frac{ \cos \left(\frac{m \phi}{4} \right) }{a} \right|^{n₂} + \left| \frac{ \sin \left(\frac{m \phi}{4} \right) }{b} \right|^{n₃} } } \end{equation}
| Variable | Effect |
|---|---|
| m | edges of shape |
| n₁ | resizes the spikes of the shape |
| n₂ | defines shape |
| n₃ | defines shape |
| a | resize cos aspect of shape |
| b | resize sin aspect of shape |
| Φ | angle from 0 … 360 (0 … 2π) |
| r | resulting distance from orgin |
Note: If A and B are different then the shape might not form a closed loop.
Sample input #
Circle #
Using these values the Superformula should give a multiple figure. The first one looking like a circle.
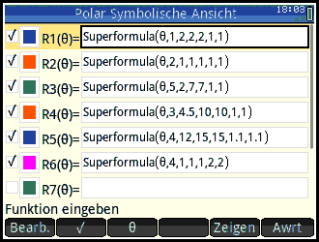
Sample output #
The program can be used in the polar plotter to get the following output.
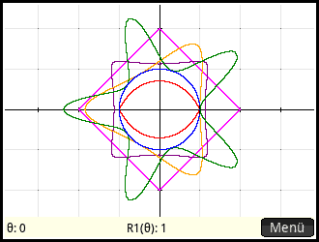
Program #
The program file contains the one programs Superformula that looks like this:
#pragma mode( separator(.,;) integer(d64) )
///
// Calculate the distance from the origin for a given angle θ. This function
// can be used with Polar-App to draw the graph of the Superformula.
//
EXPORT Superformula(θ, M, N1, N2, N3, A, B)
BEGIN
LOCAL θM := M * θ / 4;
LOCAL Retval := 1 / (N1 NTHROOT (
ABS(COS(θM) / A ) ^ N2 +
ABS(SIN(θM) / B ) ^ N3
));
RETURN Retval;
END;